




Imagen que describe la teoría de tiro parabólico en una situación de la vida común.





Se trata de un tiro parabólico simple en el que el cuerpo se lanza desde el suelo y vuelve de nuevo a él. Las fórmulas en este caso son:


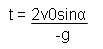
(1)
Nos dicen que la altura máxima ha de ser 100 m y el ángulo de 30º, sustituyendo entonces en la fórmula de la altura máxima y despejando la velocidad inicial



2.- Hallar a qué ángulo hay que realizar un tiro parabólico para que el alcance y la altura máxima sean iguales.
La altura máxima y el alcance han de valer exactamente lo mismo. Así pues igualando la fórmula del alcance (X) con la altura máxima (Hmax) en las ecuaciones 1 se tiene

En la ecuación se cancelan las aceleraciones de la gravedad y las velocidades iniciales, por lo que el resultado al que vamos a llegar es independiente de la velocidad a la que se realiza el lanzamiento. Resulta pues la siguiente ecuación trigonométrica

Haciendo la sustitución trigonométrica del ángulo doble
 nos queda
nos queda

Como buscamos ángulos diferentes de cero, α≠ 0, tendremos también que sinα≠0 por lo tanto podemos cancelar un factor sinα en cada miembro de la ecuación 2, que nos quedará

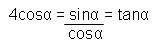


Se trata de un tiro parabólico, pero a diferencia de los anteriores el punto inicial y final no están a la misma altura con respecto al suelo por lo que las fórmulas 1 ya no son aplicables ahora. Hemos de plantearlo con las más generales que se deducen a partir de


 (3)
(3) (4)
(4)Resulta más fácil resolver el último sistema de ecuaciones despejando v0 de la ecuación 3 y sustituyendo en la ecuación 4. Calcularemos así el tiempo, pues resulta más fácil de resolver la ecuación que sale. Sustituyendo luego este tiempo en la ecuación 3 determinamos la velocidad. De la figura se ve que el alcance total del tiro parabólico es de 25+5=30m. De la ecuación 3 tenemos pues según lo dicho


el valor de t que se obtiene de esta última ecuación es

y con la ecuación 3 calculamos la velocidad inicial

El problema se podría haber resuelto directamente despejando directamente t en función de v0 lo que ocurre es que la ecuación resultante es algo más tediosa de manipular.